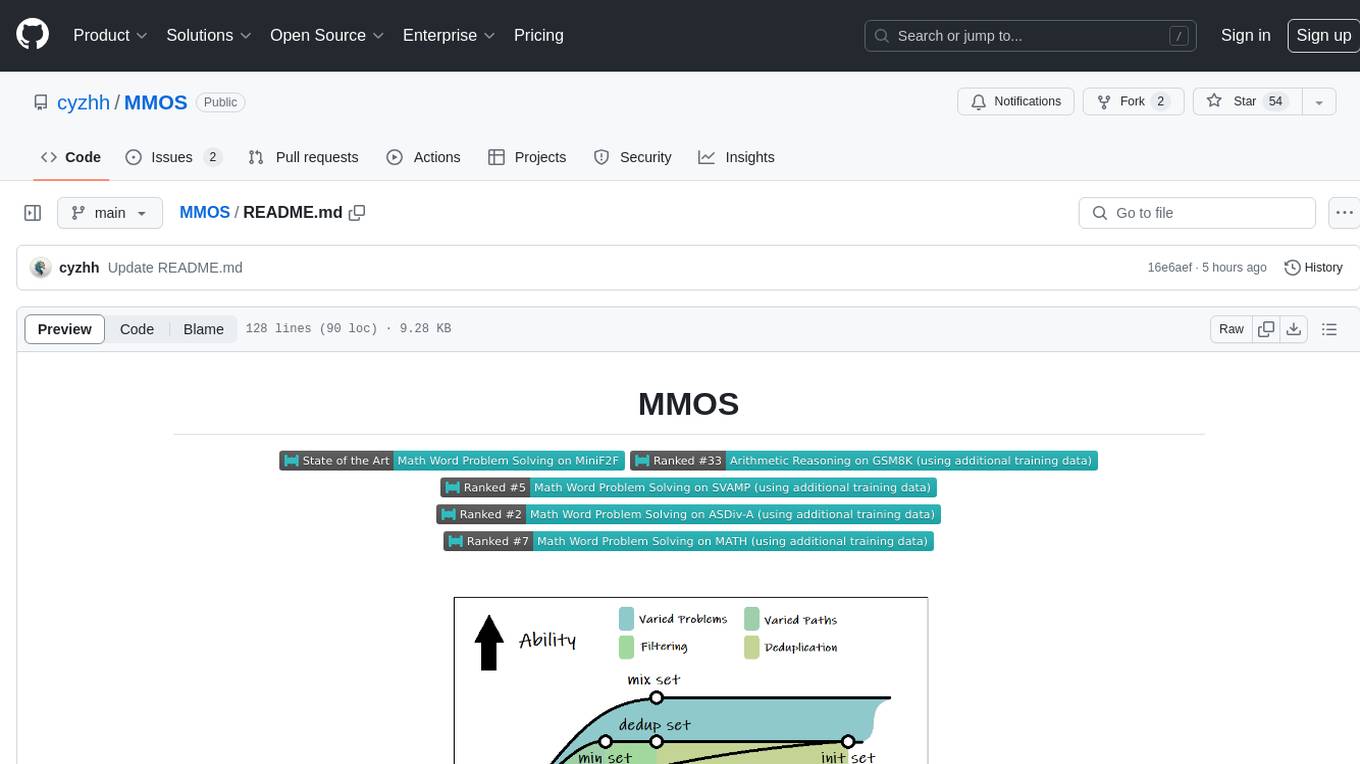
MMOS (Mix of Minimal Optimal Sets) is a dataset designed for math reasoning tasks, offering higher performance and lower construction costs. It includes various models and data subsets for tasks like arithmetic reasoning and math word problem solving. The dataset is used to identify minimal optimal sets through reasoning paths and statistical analysis, with a focus on QA-pairs generated from open-source datasets. MMOS also provides an auto problem generator for testing model robustness and scripts for training and inference.

AWQ (Activation-aware Weight Quantization) is a tool designed for efficient and accurate low-bit weight quantization (INT3/4) for Large Language Models (LLMs). It supports instruction-tuned models and multi-modal LMs, providing features such as AWQ search for accurate quantization, pre-computed AWQ model zoo for various LLMs, memory-efficient 4-bit linear in PyTorch, and efficient CUDA kernel implementation for fast inference. The tool enables users to run large models on resource-constrained edge platforms, delivering more efficient responses with LLM/VLM chatbots through 4-bit inference.

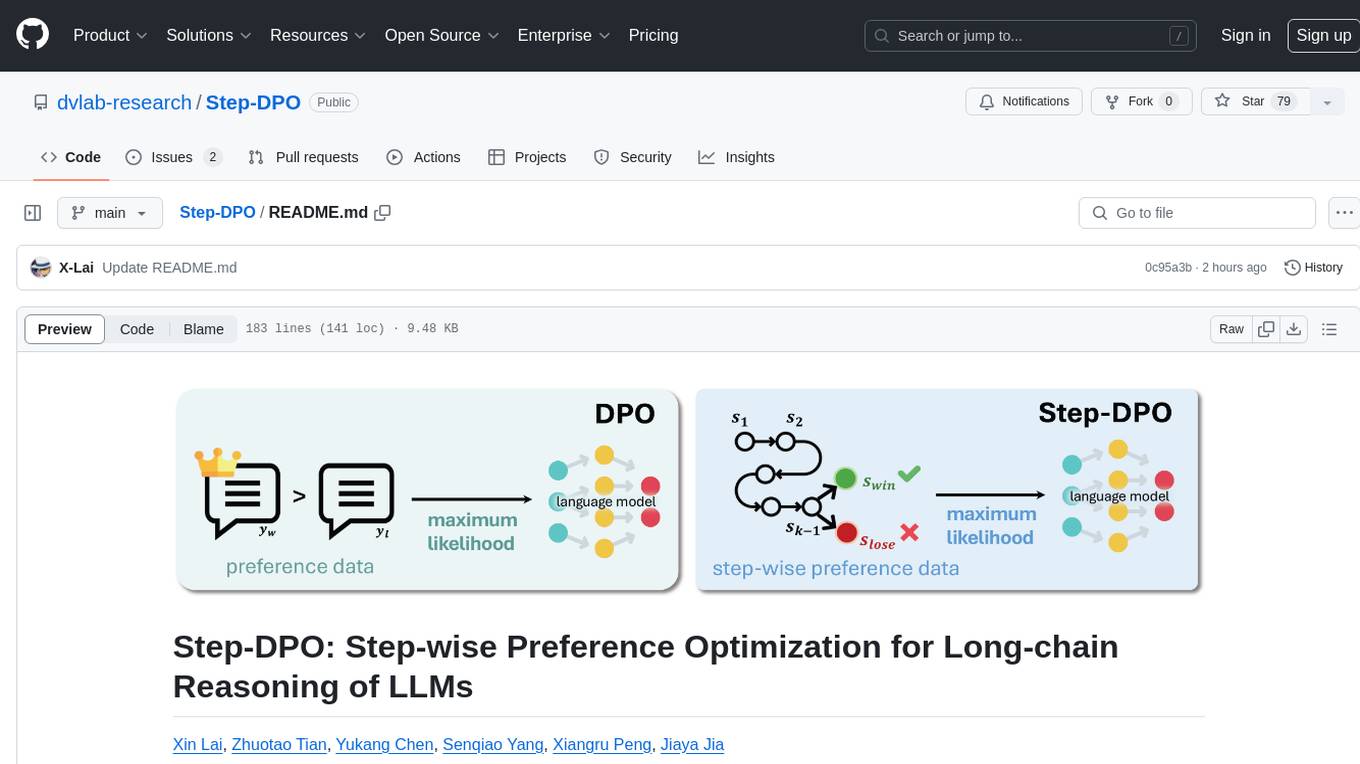
Step-DPO is a method for enhancing long-chain reasoning ability of LLMs with a data construction pipeline creating a high-quality dataset. It significantly improves performance on math and GSM8K tasks with minimal data and training steps. The tool fine-tunes pre-trained models like Qwen2-7B-Instruct with Step-DPO, achieving superior results compared to other models. It provides scripts for training, evaluation, and deployment, along with examples and acknowledgements.

This repository is a collection of resources focused on interpretability in large language models (LLMs). It aims to help beginners get started in the area and keep researchers updated on the latest progress. It includes libraries, blogs, tutorials, forums, tools, programs, papers, and more related to interpretability in LLMs.

OpenInference is a set of conventions and plugins that complement OpenTelemetry to enable tracing of AI applications. It provides a way to capture and analyze the performance and behavior of AI models, including their interactions with other components of the application. OpenInference is designed to be language-agnostic and can be used with any OpenTelemetry-compatible backend. It includes a set of instrumentations for popular machine learning SDKs and frameworks, making it easy to add tracing to your AI applications.

Speechless.AI is committed to integrating the superior language processing and deep reasoning capabilities of large language models into practical business applications. By enhancing the model's language understanding, knowledge accumulation, and text creation abilities, and introducing long-term memory, external tool integration, and local deployment, our aim is to establish an intelligent collaborative partner that can independently interact, continuously evolve, and closely align with various business scenarios.

visionOS-examples is a repository containing accelerators for Spatial Computing. It includes examples such as Local Large Language Model, Chat Apple Vision Pro, WebSockets, Anchor To Head, Hand Tracking, Battery Life, Countdown, Plane Detection, Timer Vision, and PencilKit for visionOS. The repository showcases various functionalities and features for Apple Vision Pro, offering tools for developers to enhance their visionOS apps with capabilities like hand tracking, plane detection, and real-time cryptocurrency prices.

CogVLM2 is a new generation of open source models that offer significant improvements in benchmarks such as TextVQA and DocVQA. It supports 8K content length, image resolution up to 1344 * 1344, and both Chinese and English languages. The project provides basic calling methods, fine-tuning examples, and OpenAI API format calling examples to help developers quickly get started with the model.

LLamaTuner is a repository for the Efficient Finetuning of Quantized LLMs project, focusing on building and sharing instruction-following Chinese baichuan-7b/LLaMA/Pythia/GLM model tuning methods. The project enables training on a single Nvidia RTX-2080TI and RTX-3090 for multi-round chatbot training. It utilizes bitsandbytes for quantization and is integrated with Huggingface's PEFT and transformers libraries. The repository supports various models, training approaches, and datasets for supervised fine-tuning, LoRA, QLoRA, and more. It also provides tools for data preprocessing and offers models in the Hugging Face model hub for inference and finetuning. The project is licensed under Apache 2.0 and acknowledges contributions from various open-source contributors.

This repository is a collection of papers on Tabular Large Language Models (LLMs) specialized for processing tabular data. It includes surveys, models, and applications related to table understanding tasks such as Table Question Answering, Table-to-Text, Text-to-SQL, and more. The repository categorizes the papers based on key ideas and provides insights into the advancements in using LLMs for processing diverse tables and fulfilling various tabular tasks based on natural language instructions.

This repository contains language models for the Russian language, as well as their implementation and comparison. The models are trained on a dataset of ChatGPT-generated instructions and chats in Russian. They can be used for a variety of tasks, including question answering, text generation, and translation.

Eagle is a family of Vision-Centric High-Resolution Multimodal LLMs that enhance multimodal LLM perception using a mix of vision encoders and various input resolutions. The model features a channel-concatenation-based fusion for vision experts with different architectures and knowledge, supporting up to over 1K input resolution. It excels in resolution-sensitive tasks like optical character recognition and document understanding.

A comprehensive repository focusing on 'Model Merging in LLMs, MLLMs, and Beyond', providing an exhaustive overview of model merging methods, theories, applications, and future research directions. The repository covers various advanced methods, applications in foundation models, different machine learning subfields, and tasks like pre-merging methods, architecture transformation, weight alignment, basic merging methods, and more.

NNtrainer is a software framework for training neural network models on devices with limited resources. It enables on-device fine-tuning of neural networks using user data for personalization. NNtrainer supports various machine learning algorithms and provides examples for tasks such as few-shot learning, ResNet, VGG, and product rating. It is optimized for embedded devices and utilizes CBLAS and CUBLAS for accelerated calculations. NNtrainer is open source and released under the Apache License version 2.0.

Awesome-LLMs-for-Video-Understanding is a repository dedicated to exploring Video Understanding with Large Language Models. It provides a comprehensive survey of the field, covering models, pretraining, instruction tuning, and hybrid methods. The repository also includes information on tasks, datasets, and benchmarks related to video understanding. Contributors are encouraged to add new papers, projects, and materials to enhance the repository.

MMOS (Mix of Minimal Optimal Sets) is a dataset designed for math reasoning tasks, offering higher performance and lower construction costs. It includes various models and data subsets for tasks like arithmetic reasoning and math word problem solving. The dataset is used to identify minimal optimal sets through reasoning paths and statistical analysis, with a focus on QA-pairs generated from open-source datasets. MMOS also provides an auto problem generator for testing model robustness and scripts for training and inference.

AI-TOD is a dataset for tiny object detection in aerial images, containing 700,621 object instances across 28,036 images. Objects in AI-TOD are smaller with a mean size of 12.8 pixels compared to other aerial image datasets. To use AI-TOD, download xView training set and AI-TOD_wo_xview, then generate the complete dataset using the provided synthesis tool. The dataset is publicly available for academic and research purposes under CC BY-NC-SA 4.0 license.

LLMFarm is an iOS and MacOS app designed to work with large language models (LLM). It allows users to load different LLMs with specific parameters, test the performance of various LLMs on iOS and macOS, and identify the most suitable model for their projects. The tool is based on ggml and llama.cpp by Georgi Gerganov and incorporates sources from rwkv.cpp by saharNooby, Mia by byroneverson, and LlamaChat by alexrozanski. LLMFarm features support for MacOS (13+) and iOS (16+), various inferences and sampling methods, Metal compatibility (not supported on Intel Mac), model setting templates, LoRA adapters support, LoRA finetune support, LoRA export as model support, and more. It also offers a range of inferences including LLaMA, GPTNeoX, Replit, GPT2, Starcoder, RWKV, Falcon, MPT, Bloom, and others. Additionally, it supports multimodal models like LLaVA, Obsidian, and MobileVLM. Users can customize inference options through JSON files and access supported models for download.

abliterator.py is a simple Python library/structure designed to ablate features in large language models (LLMs) supported by TransformerLens. It provides capabilities to enter temporary contexts, cache activations with N samples, calculate refusal directions, and includes tokenizer utilities. The library aims to streamline the process of experimenting with ablation direction turns by encapsulating useful logic and minimizing code complexity. While currently basic and lacking comprehensive documentation, the library serves well for personal workflows and aims to expand beyond feature ablation to augmentation and additional features over time with community support.

This repository contains assets related to AI/ML workloads on Google Kubernetes Engine (GKE). Run optimized AI/ML workloads with Google Kubernetes Engine (GKE) platform orchestration capabilities. A robust AI/ML platform considers the following layers: Infrastructure orchestration that support GPUs and TPUs for training and serving workloads at scale Flexible integration with distributed computing and data processing frameworks Support for multiple teams on the same infrastructure to maximize utilization of resources

Ray is a unified framework for scaling AI and Python applications. It consists of a core distributed runtime and a set of AI libraries for simplifying ML compute, including Data, Train, Tune, RLlib, and Serve. Ray runs on any machine, cluster, cloud provider, and Kubernetes, and features a growing ecosystem of community integrations. With Ray, you can seamlessly scale the same code from a laptop to a cluster, making it easy to meet the compute-intensive demands of modern ML workloads.

Labelbox is a data-centric AI platform for enterprises to develop, optimize, and use AI to solve problems and power new products and services. Enterprises use Labelbox to curate data, generate high-quality human feedback data for computer vision and LLMs, evaluate model performance, and automate tasks by combining AI and human-centric workflows. The academic & research community uses Labelbox for cutting-edge AI research.

Deep Java Library (DJL) is an open-source, high-level, engine-agnostic Java framework for deep learning. It is designed to be easy to get started with and simple to use for Java developers. DJL provides a native Java development experience and allows users to integrate machine learning and deep learning models with their Java applications. The framework is deep learning engine agnostic, enabling users to switch engines at any point for optimal performance. DJL's ergonomic API interface guides users with best practices to accomplish deep learning tasks, such as running inference and training neural networks.

Sweep is an AI junior developer that turns bugs and feature requests into code changes. It automatically handles developer experience improvements like adding type hints and improving test coverage.

The Teams AI Library is a software development kit (SDK) that helps developers create bots that can interact with Teams and Microsoft 365 applications. It is built on top of the Bot Framework SDK and simplifies the process of developing bots that interact with Teams' artificial intelligence capabilities. The SDK is available for JavaScript/TypeScript, .NET, and Python.

This guide is dedicated to Large Language Models (LLMs) that you can run on your home computer. It assumes your PC is a lower-end, non-gaming setup.

Supercharge WordPress Content Workflows and Engagement with Artificial Intelligence. Tap into leading cloud-based services like OpenAI, Microsoft Azure AI, Google Gemini and IBM Watson to augment your WordPress-powered websites. Publish content faster while improving SEO performance and increasing audience engagement. ClassifAI integrates Artificial Intelligence and Machine Learning technologies to lighten your workload and eliminate tedious tasks, giving you more time to create original content that matters.

Chatbot UI is an open-source AI chat app that allows users to create and deploy their own AI chatbots. It is easy to use and can be customized to fit any need. Chatbot UI is perfect for businesses, developers, and anyone who wants to create a chatbot.

BricksLLM is a cloud native AI gateway written in Go. Currently, it provides native support for OpenAI, Anthropic, Azure OpenAI and vLLM. BricksLLM aims to provide enterprise level infrastructure that can power any LLM production use cases. Here are some use cases for BricksLLM: * Set LLM usage limits for users on different pricing tiers * Track LLM usage on a per user and per organization basis * Block or redact requests containing PIIs * Improve LLM reliability with failovers, retries and caching * Distribute API keys with rate limits and cost limits for internal development/production use cases * Distribute API keys with rate limits and cost limits for students

uAgents is a Python library developed by Fetch.ai that allows for the creation of autonomous AI agents. These agents can perform various tasks on a schedule or take action on various events. uAgents are easy to create and manage, and they are connected to a fast-growing network of other uAgents. They are also secure, with cryptographically secured messages and wallets.

Griptape is a modular Python framework for building AI-powered applications that securely connect to your enterprise data and APIs. It offers developers the ability to maintain control and flexibility at every step. Griptape's core components include Structures (Agents, Pipelines, and Workflows), Tasks, Tools, Memory (Conversation Memory, Task Memory, and Meta Memory), Drivers (Prompt and Embedding Drivers, Vector Store Drivers, Image Generation Drivers, Image Query Drivers, SQL Drivers, Web Scraper Drivers, and Conversation Memory Drivers), Engines (Query Engines, Extraction Engines, Summary Engines, Image Generation Engines, and Image Query Engines), and additional components (Rulesets, Loaders, Artifacts, Chunkers, and Tokenizers). Griptape enables developers to create AI-powered applications with ease and efficiency.