This repository contains the source code for a GEMM & deep learning hardware accelerator system used to validate proposed systolic array hardware architectures implementing efficient matrix multiplication algorithms to increase performance-per-area limits of GEMM & AI accelerators. Achieved results include up to 3× faster CNN inference, >2× higher mults/multiplier/clock cycle, and low area with high clock frequency. The system is specialized for inference of non-sparse DNN models with fixed-point/quantized inputs, fully accelerating all DNN layers in hardware, and highly optimizing GEMM acceleration.

NanoFlow is a throughput-oriented high-performance serving framework for Large Language Models (LLMs) that consistently delivers superior throughput compared to other frameworks by utilizing key techniques such as intra-device parallelism, asynchronous CPU scheduling, and SSD offloading. The framework proposes nano-batching to schedule compute-, memory-, and network-bound operations for simultaneous execution, leading to increased resource utilization. NanoFlow also adopts an asynchronous control flow to optimize CPU overhead and eagerly offloads KV-Cache to SSDs for multi-round conversations. The open-source codebase integrates state-of-the-art kernel libraries and provides necessary scripts for environment setup and experiment reproduction.

LLM-D is a machine learning model for sentiment analysis. It is designed to classify text data into positive, negative, or neutral sentiment categories. The model is trained on a large dataset of labeled text samples and uses natural language processing techniques to analyze and predict sentiment in new text inputs. LLM-D is a powerful tool for businesses and researchers looking to understand customer feedback, social media sentiment, and other text data sources. It can be easily integrated into existing applications or used as a standalone tool for sentiment analysis tasks.

Unified Cache Manager (UCM) is a tool designed to persist the LLM KVCache and replace redundant computations through various retrieval mechanisms. It supports prefix caching and offers training-free sparse attention retrieval methods, enhancing performance for long sequence inference tasks. UCM also provides a PD disaggregation solution based on a storage-compute separation architecture, enabling easier management of heterogeneous computing resources. When integrated with vLLM, UCM significantly reduces inference latency in scenarios like multi-turn dialogue and long-context reasoning tasks.

LongRoPE is a method to extend the context window of large language models (LLMs) beyond 2 million tokens. It identifies and exploits non-uniformities in positional embeddings to enable 8x context extension without fine-tuning. The method utilizes a progressive extension strategy with 256k fine-tuning to reach a 2048k context. It adjusts embeddings for shorter contexts to maintain performance within the original window size. LongRoPE has been shown to be effective in maintaining performance across various tasks from 4k to 2048k context lengths.

MemoryBear is a next-generation AI memory system developed by RedBear AI, focusing on overcoming limitations in knowledge storage and multi-agent collaboration. It empowers AI with human-like memory capabilities, enabling deep knowledge understanding and cognitive collaboration. The system addresses challenges such as knowledge forgetting, memory gaps in multi-agent collaboration, and semantic ambiguity during reasoning. MemoryBear's core features include memory extraction engine, graph storage, hybrid search, memory forgetting engine, self-reflection engine, and FastAPI services. It offers a standardized service architecture for efficient integration and invocation across applications.

ReaLHF is a distributed system designed for efficient RLHF training with Large Language Models (LLMs). It introduces a novel approach called parameter reallocation to dynamically redistribute LLM parameters across the cluster, optimizing allocations and parallelism for each computation workload. ReaL minimizes redundant communication while maximizing GPU utilization, achieving significantly higher Proximal Policy Optimization (PPO) training throughput compared to other systems. It supports large-scale training with various parallelism strategies and enables memory-efficient training with parameter and optimizer offloading. The system seamlessly integrates with HuggingFace checkpoints and inference frameworks, allowing for easy launching of local or distributed experiments. ReaLHF offers flexibility through versatile configuration customization and supports various RLHF algorithms, including DPO, PPO, RAFT, and more, while allowing the addition of custom algorithms for high efficiency.

This repository is a work in progress that contains first-principle implementations of groundbreaking AI algorithms using various deep learning frameworks. Each implementation is accompanied by supporting research papers, aiming to provide comprehensive educational resources for understanding and implementing foundational AI algorithms from scratch.

EScAIP is an Efficiently Scaled Attention Interatomic Potential that leverages a novel multi-head self-attention formulation within graph neural networks to predict energy and forces between atoms in molecules and materials. It achieves substantial gains in efficiency, at least 10x speed up in inference time and 5x less memory usage compared to existing models. EScAIP represents a philosophy towards developing general-purpose Neural Network Interatomic Potentials that achieve better expressivity through scaling and continue to scale efficiently with increased computational resources and training data.

GLake is an acceleration library and utilities designed to optimize GPU memory management and IO transmission for AI large model training and inference. It addresses challenges such as GPU memory bottleneck and IO transmission bottleneck by providing efficient memory pooling, sharing, and tiering, as well as multi-path acceleration for CPU-GPU transmission. GLake is easy to use, open for extension, and focuses on improving training throughput, saving inference memory, and accelerating IO transmission. It offers features like memory fragmentation reduction, memory deduplication, and built-in security mechanisms for troubleshooting GPU memory issues.

siiRL is a novel, fully distributed reinforcement learning (RL) framework designed to break the scaling barriers in Large Language Models (LLMs) post-training. Developed by researchers from Shanghai Innovation Institute, siiRL delivers near-linear scalability, dramatic throughput gains, and unprecedented flexibility for RL-based LLM development. It eliminates the centralized controller common in other frameworks, enabling scalability to thousands of GPUs, achieving state-of-the-art throughput, and supporting cross-hardware compatibility. siiRL is extensively benchmarked and excels in data-intensive workloads such as long-context and multi-modal training.

Ianvs is a distributed synergy AI benchmarking project incubated in KubeEdge SIG AI. It aims to test the performance of distributed synergy AI solutions following recognized standards, providing end-to-end benchmark toolkits, test environment management tools, test case control tools, and benchmark presentation tools. It also collaborates with other organizations to establish comprehensive benchmarks and related applications. The architecture includes critical components like Test Environment Manager, Test Case Controller, Generation Assistant, Simulation Controller, and Story Manager. Ianvs documentation covers quick start, guides, dataset descriptions, algorithms, user interfaces, stories, and roadmap.

Llumnix is a cross-instance request scheduling layer built on top of LLM inference engines such as vLLM, providing optimized multi-instance serving performance with low latency, reduced time-to-first-token (TTFT) and queuing delays, reduced time-between-tokens (TBT) and preemption stalls, and high throughput. It achieves this through dynamic, fine-grained, KV-cache-aware scheduling, continuous rescheduling across instances, KV cache migration mechanism, and seamless integration with existing multi-instance deployment platforms. Llumnix is easy to use, fault-tolerant, elastic, and extensible to more inference engines and scheduling policies.

The LLM course is divided into three parts: 1. 🧩 **LLM Fundamentals** covers essential knowledge about mathematics, Python, and neural networks. 2. 🧑‍🔬 **The LLM Scientist** focuses on building the best possible LLMs using the latest techniques. 3. 👷 **The LLM Engineer** focuses on creating LLM-based applications and deploying them. For an interactive version of this course, I created two **LLM assistants** that will answer questions and test your knowledge in a personalized way: * 🤗 **HuggingChat Assistant**: Free version using Mixtral-8x7B. * 🤖 **ChatGPT Assistant**: Requires a premium account. ## 📝 Notebooks A list of notebooks and articles related to large language models. ### Tools | Notebook | Description | Notebook | |----------|-------------|----------| | 🧐 LLM AutoEval | Automatically evaluate your LLMs using RunPod |  | | 🥱 LazyMergekit | Easily merge models using MergeKit in one click. |  | | 🦎 LazyAxolotl | Fine-tune models in the cloud using Axolotl in one click. |  | | ⚡ AutoQuant | Quantize LLMs in GGUF, GPTQ, EXL2, AWQ, and HQQ formats in one click. |  | | 🌳 Model Family Tree | Visualize the family tree of merged models. |  | | 🚀 ZeroSpace | Automatically create a Gradio chat interface using a free ZeroGPU. |  |

At Nesa, privacy is a critical objective. Equivariant Encryption (EE) is a solution developed to perform inference on neural networks without exposing input and output data. EE integrates specialized transformations for neural networks, maintaining data privacy while ensuring inference operates correctly on encrypted inputs. It provides the same latency as plaintext inference with no slowdowns and offers strong security guarantees. EE avoids the computational costs of traditional Homomorphic Encryption (HE) by preserving non-linear neural functions. The tool is designed for modern neural architectures, ensuring accuracy, scalability, and compatibility with existing pipelines.

Awesome OpenVINO is a curated list of AI projects based on the OpenVINO toolkit, offering a rich assortment of projects, libraries, and tutorials covering various topics like model optimization, deployment, and real-world applications across industries. It serves as a valuable resource continuously updated to maximize the potential of OpenVINO in projects, featuring projects like Stable Diffusion web UI, Visioncom, FastSD CPU, OpenVINO AI Plugins for GIMP, and more.

This repository contains the source code for a GEMM & deep learning hardware accelerator system used to validate proposed systolic array hardware architectures implementing efficient matrix multiplication algorithms to increase performance-per-area limits of GEMM & AI accelerators. Achieved results include up to 3× faster CNN inference, >2× higher mults/multiplier/clock cycle, and low area with high clock frequency. The system is specialized for inference of non-sparse DNN models with fixed-point/quantized inputs, fully accelerating all DNN layers in hardware, and highly optimizing GEMM acceleration.

SPEAR (Simulator for Photorealistic Embodied AI Research) is a powerful tool for training embodied agents. It features 300 unique virtual indoor environments with 2,566 unique rooms and 17,234 unique objects that can be manipulated individually. Each environment is designed by a professional artist and features detailed geometry, photorealistic materials, and a unique floor plan and object layout. SPEAR is implemented as Unreal Engine assets and provides an OpenAI Gym interface for interacting with the environments via Python.

OpenVINO™ is an open-source toolkit for optimizing and deploying AI inference. It provides a common API to deliver inference solutions on various platforms, including CPU, GPU, NPU, and heterogeneous devices. OpenVINO™ supports pre-trained models from Open Model Zoo and popular frameworks like TensorFlow, PyTorch, and ONNX. Key components of OpenVINO™ include the OpenVINO™ Runtime, plugins for different hardware devices, frontends for reading models from native framework formats, and the OpenVINO Model Converter (OVC) for adjusting models for optimal execution on target devices.

PEFT (Parameter-Efficient Fine-Tuning) is a collection of state-of-the-art methods that enable efficient adaptation of large pretrained models to various downstream applications. By only fine-tuning a small number of extra model parameters instead of all the model's parameters, PEFT significantly decreases the computational and storage costs while achieving performance comparable to fully fine-tuned models.

This repo hosts tutorial documentation for running generative AI models on NVIDIA Jetson devices. The documentation is auto-generated and hosted on GitHub Pages using their CI/CD feature to automatically generate/update the HTML documentation site upon new commits.

Emgu CV is a cross-platform .Net wrapper for the OpenCV image-processing library. It allows OpenCV functions to be called from .NET compatible languages. The wrapper can be compiled by Visual Studio, Unity, and "dotnet" command, and it can run on Windows, Mac OS, Linux, iOS, and Android.

MMStar is an elite vision-indispensable multi-modal benchmark comprising 1,500 challenge samples meticulously selected by humans. It addresses two key issues in current LLM evaluation: the unnecessary use of visual content in many samples and the existence of unintentional data leakage in LLM and LVLM training. MMStar evaluates 6 core capabilities across 18 detailed axes, ensuring a balanced distribution of samples across all dimensions.

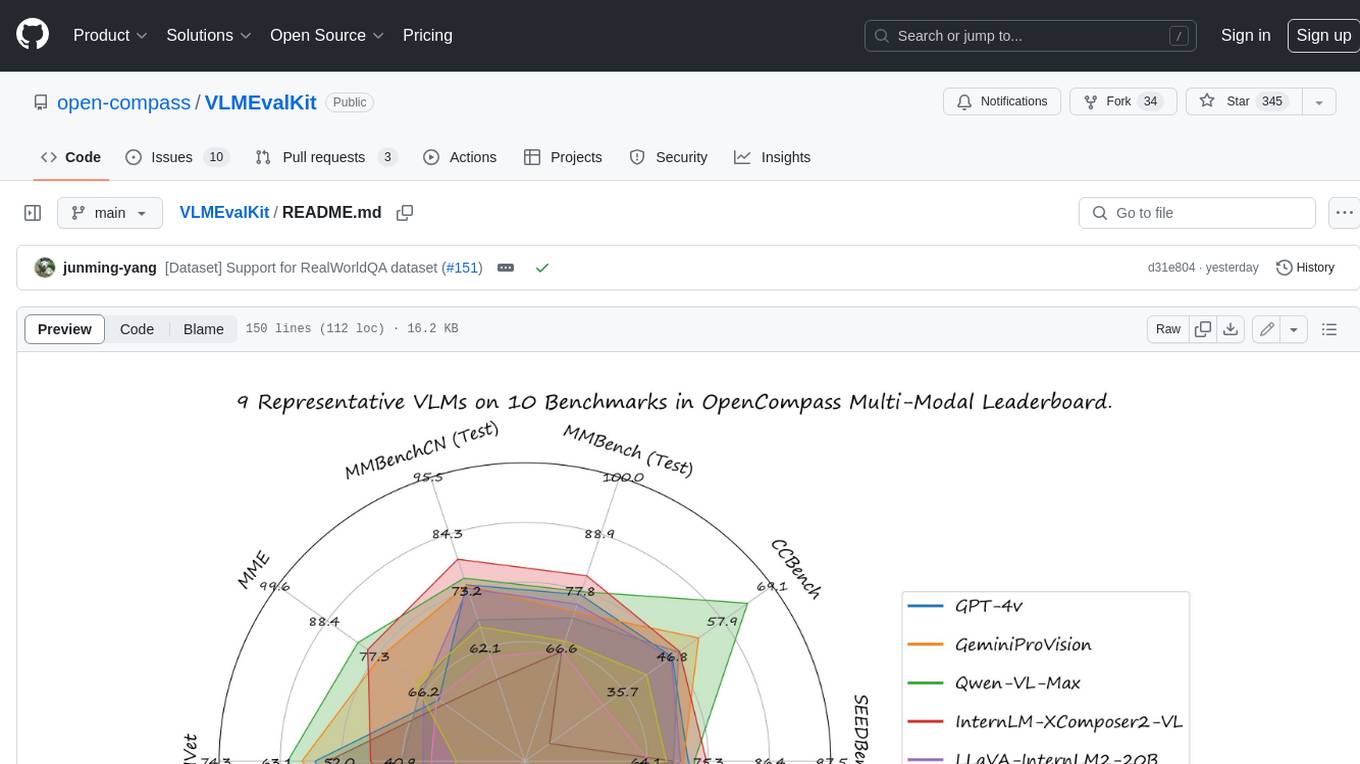
VLMEvalKit is an open-source evaluation toolkit of large vision-language models (LVLMs). It enables one-command evaluation of LVLMs on various benchmarks, without the heavy workload of data preparation under multiple repositories. In VLMEvalKit, we adopt generation-based evaluation for all LVLMs, and provide the evaluation results obtained with both exact matching and LLM-based answer extraction.

This Docker image for LLaVA (Large Language and Vision Assistant) provides a convenient way to run LLaVA locally or on RunPod. LLaVA is a powerful AI tool that combines natural language processing and computer vision capabilities. With this Docker image, you can easily access LLaVA's functionalities for various tasks, including image captioning, visual question answering, text summarization, and more. The image comes pre-installed with LLaVA v1.2.0, Torch 2.1.2, xformers 0.0.23.post1, and other necessary dependencies. You can customize the model used by setting the MODEL environment variable. The image also includes a Jupyter Lab environment for interactive development and exploration. Overall, this Docker image offers a comprehensive and user-friendly platform for leveraging LLaVA's capabilities.