
LeanAide
Tools based on AI for helping with Lean 4
Stars: 97
LeanAide is a work in progress AI tool designed to assist with development using the Lean Theorem Prover. It currently offers a tool that translates natural language statements to Lean types, including theorem statements. The tool is based on GPT 3.5-turbo/GPT 4 and requires an OpenAI key for usage. Users can include LeanAide as a dependency in their projects to access the translation functionality.
README:
LeanAide or LeanAIde (accidental pun) is work in progress to build AI based tools to help development with the Lean Theorem Prover. The core technique we use is Autoformalization which is the process of translating informal mathematical statements to formal statements in a proof assistant. This is used both directly to provide tools and indirectly to generate proofs by translation from natural language proofs generated by Large Language models.
We now (as of early February 2025, modified September 2025) have a convenient way to use LeanAide in your own projects, using a server-client setup which we outline below.
The most convenient way to use LeanAide is with syntax we provide that gives code-actions. We have syntax for translating theorems and definitions from natural language to Lean, and for adding documentation strings to theorems and definitions. For example, the following code in a Lean file (with correct dependencies) will give code actions:
import LeanAideTools
import Mathlib
#theorem "There are infinitely many odd numbers"
#def "A number is defined to be cube-free if it is not divisible by the cube of a prime number"
#doc
theorem InfiniteOddNumbers : {n ∣ Odd n}.Infinite := by sorryWe also provide syntax for generating/completing proofs. For now this is slow and not of good quality. Experiments and feedback are welcome. The first of the examples below uses a command and the second uses a tactic.
#prove "The product of two successive natural numbers is even"To either experiment directly with LeanAide or use it via the server-client setup as a dependency in your own project, you need to first install LeanAide.
First clone the repository. Next, from the root of the repository, run the following commands to build and fetch pre-loaded embeddings:
lake exe cache get # download prebuilt mathlib binaries
lake build mathlib
lake build
lake exe fetch_embeddingsOur translation is based on GPT 4o from OpenAI, but you can use alternative models (including local ones). Note that we also use embeddings from OpenAI, so you will need an OpenAI API key unless you set up an example server as descried below. Here, we assume you have an OpenAI API key.
To get started please configure environment variables using the following bash commands or equivalent in your system at the base of the repository (the angle brackets are not to be included in the command), and then launch VS code.
export OPENAI_API_KEY=<your-open-ai-key>
code .Alternatively, you can create a file with path private/OPENAI_API_KEY (relative to the root of LeanAIDE) containing your key.
After this open the folder in VS code (or equivalent) with Lean 4 and go to the file LeanCodePrompts/TranslateDemo.lean. Any statement written using syntax
similar to #theorem "There are infinitely many primes" will be translated into Lean code. You will see examples of this in the demo files. Once the translation is done, a Try this hyperlink and code-action will appear. Clicking on this will add the translated code to the file.
Alternatively, you can translate a statement using the following command in the Lean REPL:
lake exe translate "There are infinitely many primes"Adding LeanAide as a dependency to your project is brittle and slow. In particular, toolchains need to match exactly. Further, there may be a collision of transitive dependencies.
We provide a server-client setup that is more robust and faster, based on the zero-dependency sub-project LeanAideCore, which is the corresponding folder in this repository (and a dependency of LeanAide). This can act as a client to the server in this repository.
The simplest (and we expect the most common) way to set up LeanAide to use in your project is to run a server locally. To do this, first set up LeanAide as described above. Then run the following command from the root of the repository:
python3 leanaide_server.pyWe assume you have Python 3 installed but we only use builtin packages. There is a nicer interactive version of the server. To use this, install the packages in server/requirements.txt and start the server with the "--ui" parameter.
python3 leanaide_server.py --uiIf you wish to use a different model supporting the OpenAI API, you can pass parameters as in the following example where we use the Mistral API. To use a local model, you can run with the OpenAI Chat API using, for example vLLM and give a local url.
python3 leanaide_server.py --url https://api.mistral.ai/v1/chat/completions --auth_key <Mistral API key> --model "mistral-small-latest"Next, add LeanAideCore as a dependency to your project. This can be done by adding the following line to your lakefile.toml file:
[[require]]
name = "leanaidecore"
git = "https://github.com/siddhartha-gadgil/LeanAide.git"
rev = "main"
subDir = "LeanAideCore"If you use a lakefile.lean file, you can add the following line to the file:
require "leanaidecore" from git "https://github.com/siddhartha-gadgil/LeanAide.git" @ "main" / "LeanAideCore"Now you can use the LeanAideCore package in your project. The following is an example of how to use it:
import LeanAideTools
import Mathlib -- as the translated/generated code is likely to use it
#leanaide_connect -- also start a server as above.
#theorem "There are infinitely many primes."Generating proofs and Autoformalization of documents is still very experimental. All are welcome to experiment (and let us know what breaks).
Our approach to proving (and formalization of proofs and documents) is to do this in multiple steps. We have various stages of a proof, with corresponding types:
-
TheoremText: The statement of a theorem and optionally a name. We can use a string in place of this. -
TheoremCode: This is generated by translation of statements.- The statement of a theorem.
- A name for the theorem.
- The type as a Lean Expression.
- A Lean command defining the theorem, with the proof usually
by sorry.
-
ProofDocument: This has a name and text "content". It is generated by an LLM based on detailed instructions including those making it suitable for formalization in Lean and relevant Lean definitions included. -
StructuredProof: This has name and a document in a custom JSON schema designed for formalization. This is generated from aProofDocumentby an LLM given the schema. -
ProofCode: This is Lean code for the theorems and proofs (in general withsorryin proofs). This is generated from the structured proof using translations of statements and definitions along with Lean meta-programming to build the code from the pieces, and tactics likesimp,aesop,hammerandgrindto finish proofs.
We have syntax to generate any later stage of the above from an earlier stage. For example, suppose (in the setup as above) you type the following command:
#prove "The inverse of the identity element in a group is the identity element"You will be offered code actions (including hyperlinks) to commands of the following format:
#prove "The inverse of the identity element in a group is the identity element" >> <target-type>If one chooses (or directly enters) StructuredProof as the target type, then an element is generated of this type. For convenience some additional syntax has been introduced to represent terms of some of these types.
To experiment from some other language (or even the command line), one can directly POST Json to the server and handle the JSON output. Indeed the server is a thin wrapper around the lean executable leanaide_process.lean, so one can start this with lake exe leanaide_process.lean and use stdio/stdin.
The JSON for each task has a "task" field with the name of the task and should have the other fields required by the task. One can also chain tasks by having a "tasks" field which is a list of tasks instead of the "task" field. In this case the output of each task is merged with its input and becomes the input of the next task.
The tasks supported are the following:
-
translate_thm— Translate a natural-language theorem into Lean and elaborate its type-
Inputs:
-
theorem_text : String— natural-language statement of the theorem
-
-
Outputs:
-
Except (Array ElabError) Expr— either a successfully elaborated theorem type (Expr) or a list of elaboration errors
-
-
-
translate_thm_detailed— Translate a natural-language theorem with name and produce Lean declaration-
Inputs:
-
theorem_text : String— natural-language statement -
theorem_name : Option Name— optional name to assign to the theorem
-
-
Outputs:
-
(Name × Expr × Syntax.Command)-
Name— theorem name -
Expr— elaborated type of the theorem -
Syntax.Command— Lean command syntax for the full theorem declaration
-
-
-
-
translate_def— Translate a natural-language definition into Lean code-
Inputs:
-
definition_text : String— natural-language definition
-
-
Outputs:
-
Except (Array CmdElabError) Syntax.Command— either a Lean definition command or elaboration errors
-
-
-
theorem_doc— Generate natural-language documentation for a theorem-
Inputs:
-
theorem_name : Name— name of the theorem -
theorem_statement : Syntax.Command— Lean syntax of the theorem statement
-
-
Outputs:
-
String— natural-language documentation of the theorem
-
-
-
def_doc— Generate natural-language documentation for a definition-
Inputs:
-
definition_name : Name— name of the definition -
definition_code : Syntax.Command— Lean syntax of the definition
-
-
Outputs:
-
String— natural-language documentation for the definition
-
-
-
theorem_name— Generate a Lean Prover name for the theorem-
Inputs:
-
theorem_text : String— natural-language statement
-
-
Outputs:
-
Name— automatically generated Lean name for the theorem
-
-
-
prove_for_formalization— Generate a detailed proof or proof sketch for a theorem-
Inputs:
-
theorem_text : String— natural-language theorem -
theorem_code : Expr— elaborated theorem type -
theorem_statement : Syntax.Command— full Lean statement
-
-
Outputs:
-
String— a document (likely a natural-language or partially formal proof)
-
-
-
json_structured— Convert a natural-language document into a structured JSON representation-
Inputs:
-
document_text : String— some natural-language math text
-
-
Outputs:
-
Json— structured JSON representation of the document
-
-
-
lean_from_json_structured— Generate Lean code from structured JSON-
Inputs:
-
document_json : Json— structured JSON of a document
-
-
Outputs:
-
TSyntax ``commandSeq— Lean code parsed from the JSON
-
-
-
elaborate— Elaborate Lean code and collect results, logs, and unsolved goals-
Inputs:
-
document_code : String— Lean code (as text)
-
-
Outputs:
-
CodeElabResult— structured result with:-
declarations : List Name— names of elaborated declarations -
logs : List String— log messages -
sorries : List (Name × Expr)— unproven obligations -
sorriesAfterPurge : List (Name × Expr)— remaining obligations after simplification
-
-
-
-
math_query— Answer a math question in natural language-
Inputs:
-
query : String— math question -
history : List ChatPair(optional, default[]) — conversation context -
n : Nat(optional, default3) — number of answers to generate
-
-
Outputs:
-
List String— candidate answers to the math question
-
-
The server is by default launched at http://localhost:7654. This can be customized by setting the variables HOST and LEANAIDE_PORT. To use a shared server, simply set HOST to the IP of the hosting machine. In the client, i.e., the project with LeanAideCore as a dependency, replace the #leanaide_connect with the following.
#leanaide_connect <hosts IP address>:7654to use the host. Further, unless you want all clients to use the hosts authentication for OpenAI or whatever is the model used, the host should not specify an authentication key (better still, start the server with --auth_key "A key that will not work"). The client should then supply the authentication key with
set_option leanaide.authkey? "<authentication-key>"There are many other configurations at the server and client end.
If you wish to use embeddings different from the OpenAI embeddings, for example for a fully open-source solution, you can run an "examples server" and set the parameter examples_url to point to it. We provide a basic implementation of this in the example_server directory. To start this, run the following:
cd example_server
python3 prebuild_embeddings
flask runThe second command should be run only the first time you set up. Once you start the server, set examples_url = "localhost:5000/find_nearest" to use the embedding server.
The file example_server/README.md sketches the configuration options and also the protocol in case you wish to make a fully customized embedding database.
The principal author of this repository is Siddhartha Gadgil.
The first phase of this work (roughly June 2022-October 2023) was done in collaboration with:
- Anand Rao Tadipatri
- Ayush Agrawal
- Ashvni Narayanan
- Navin Goyal
We had a lot of help from the Lean community and from collaborators at Microsoft Research. Our server is hosted with support from research credits from Google.
More recently (since about October 2024) the work has been done in collaboration with:
- Anirudh Gupta
- Vaishnavi Shirsath
- Ajay Kumar Nair
- Malhar Patel
- Sushrut Jog
This is supported by ARCNet, ART-PARK, IISc.
Our work is described in a note at the 2nd Math AI workshop and in more detail (along with related work) in a preprint.
For Tasks:
Click tags to check more tools for each tasksFor Jobs:
Alternative AI tools for LeanAide
Similar Open Source Tools

LeanAide
LeanAide is a work in progress AI tool designed to assist with development using the Lean Theorem Prover. It currently offers a tool that translates natural language statements to Lean types, including theorem statements. The tool is based on GPT 3.5-turbo/GPT 4 and requires an OpenAI key for usage. Users can include LeanAide as a dependency in their projects to access the translation functionality.
LongRAG
This repository contains the code for LongRAG, a framework that enhances retrieval-augmented generation with long-context LLMs. LongRAG introduces a 'long retriever' and a 'long reader' to improve performance by using a 4K-token retrieval unit, offering insights into combining RAG with long-context LLMs. The repo provides instructions for installation, quick start, corpus preparation, long retriever, and long reader.
py-vectara-agentic
The `vectara-agentic` Python library is designed for developing powerful AI assistants using Vectara and Agentic-RAG. It supports various agent types, includes pre-built tools for domains like finance and legal, and enables easy creation of custom AI assistants and agents. The library provides tools for summarizing text, rephrasing text, legal tasks like summarizing legal text and critiquing as a judge, financial tasks like analyzing balance sheets and income statements, and database tools for inspecting and querying databases. It also supports observability via LlamaIndex and Arize Phoenix integration.
warc-gpt
WARC-GPT is an experimental retrieval augmented generation pipeline for web archive collections. It allows users to interact with WARC files, extract text, generate text embeddings, visualize embeddings, and interact with a web UI and API. The tool is highly customizable, supporting various LLMs, providers, and embedding models. Users can configure the application using environment variables, ingest WARC files, start the server, and interact with the web UI and API to search for content and generate text completions. WARC-GPT is designed for exploration and experimentation in exploring web archives using AI.
vulnerability-analysis
The NVIDIA AI Blueprint for Vulnerability Analysis for Container Security showcases accelerated analysis on common vulnerabilities and exposures (CVE) at an enterprise scale, reducing mitigation time from days to seconds. It enables security analysts to determine software package vulnerabilities using large language models (LLMs) and retrieval-augmented generation (RAG). The blueprint is designed for security analysts, IT engineers, and AI practitioners in cybersecurity. It requires NVAIE developer license and API keys for vulnerability databases, search engines, and LLM model services. Hardware requirements include L40 GPU for pipeline operation and optional LLM NIM and Embedding NIM. The workflow involves LLM pipeline for CVE impact analysis, utilizing LLM planner, agent, and summarization nodes. The blueprint uses NVIDIA NIM microservices and Morpheus Cybersecurity AI SDK for vulnerability analysis.
MiniAgents
MiniAgents is an open-source Python framework designed to simplify the creation of multi-agent AI systems. It offers a parallelism and async-first design, allowing users to focus on building intelligent agents while handling concurrency challenges. The framework, built on asyncio, supports LLM-based applications with immutable messages and seamless asynchronous token and message streaming between agents.

appworld
AppWorld is a high-fidelity execution environment of 9 day-to-day apps, operable via 457 APIs, populated with digital activities of ~100 people living in a simulated world. It provides a benchmark of natural, diverse, and challenging autonomous agent tasks requiring rich and interactive coding. The repository includes implementations of AppWorld apps and APIs, along with tests. It also introduces safety features for code execution and provides guides for building agents and extending the benchmark.
safety-tooling
This repository, safety-tooling, is designed to be shared across various AI Safety projects. It provides an LLM API with a common interface for OpenAI, Anthropic, and Google models. The aim is to facilitate collaboration among AI Safety researchers, especially those with limited software engineering backgrounds, by offering a platform for contributing to a larger codebase. The repo can be used as a git submodule for easy collaboration and updates. It also supports pip installation for convenience. The repository includes features for installation, secrets management, linting, formatting, Redis configuration, testing, dependency management, inference, finetuning, API usage tracking, and various utilities for data processing and experimentation.
honcho
Honcho is a platform for creating personalized AI agents and LLM powered applications for end users. The repository is a monorepo containing the server/API for managing database interactions and storing application state, along with a Python SDK. It utilizes FastAPI for user context management and Poetry for dependency management. The API can be run using Docker or manually by setting environment variables. The client SDK can be installed using pip or Poetry. The project is open source and welcomes contributions, following a fork and PR workflow. Honcho is licensed under the AGPL-3.0 License.
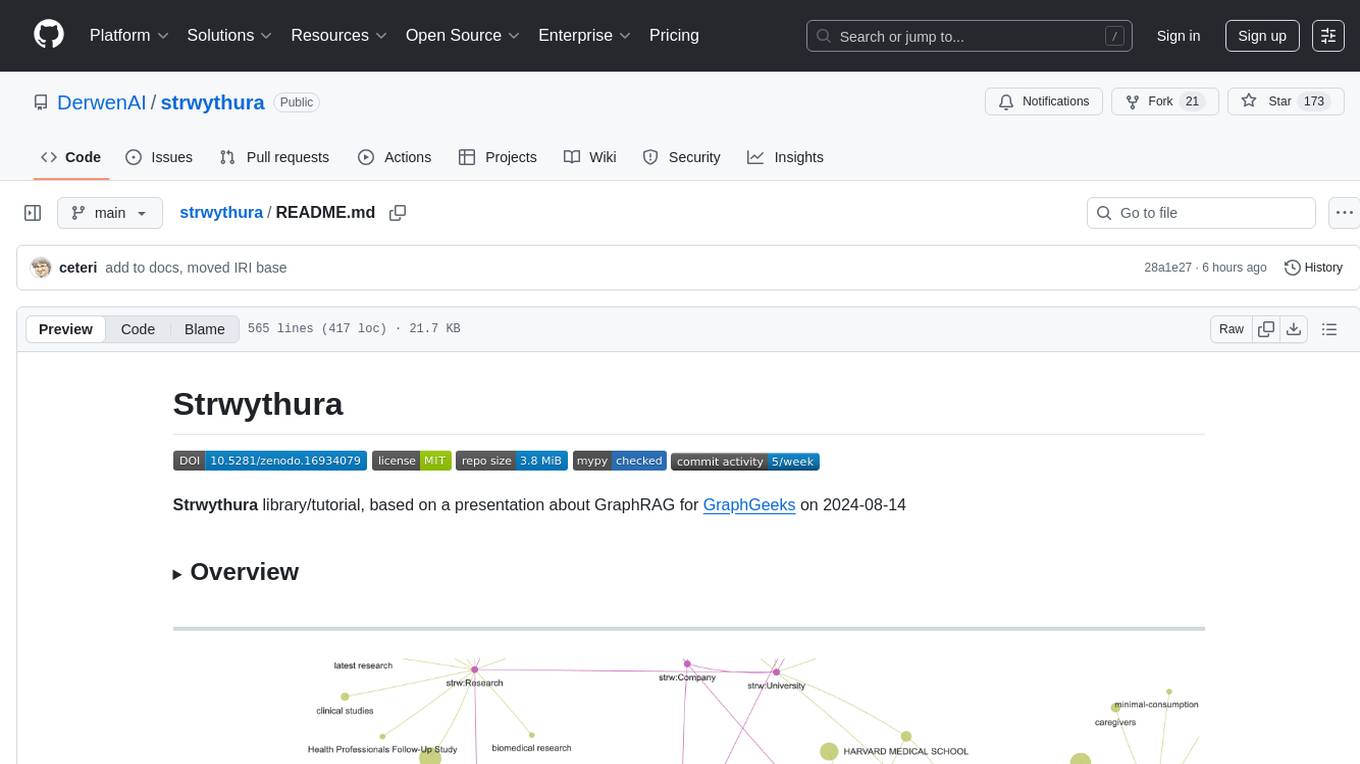
strwythura
Strwythura is a library and tutorial focused on constructing a knowledge graph from unstructured data sources using state-of-the-art models for named entity recognition. It implements an enhanced GraphRAG approach and curates semantics for optimizing AI application outcomes within a specific domain. The tutorial emphasizes the use of sophisticated NLP pipelines based on spaCy, GLiNER, TextRank, and related libraries to provide better/faster/cheaper results with more control over the intentional arrangement of the knowledge graph. It leverages neurosymbolic AI methods and combines practices from natural language processing, graph data science, entity resolution, ontology pipeline, context engineering, and human-in-the-loop processes.
PolyMind
PolyMind is a multimodal, function calling powered LLM webui designed for various tasks such as internet searching, image generation, port scanning, Wolfram Alpha integration, Python interpretation, and semantic search. It offers a plugin system for adding extra functions and supports different models and endpoints. The tool allows users to interact via function calling and provides features like image input, image generation, and text file search. The application's configuration is stored in a `config.json` file with options for backend selection, compatibility mode, IP address settings, API key, and enabled features.
mflux
MFLUX is a line-by-line port of the FLUX implementation in the Huggingface Diffusers library to Apple MLX. It aims to run powerful FLUX models from Black Forest Labs locally on Mac machines. The codebase is minimal and explicit, prioritizing readability over generality and performance. Models are implemented from scratch in MLX, with tokenizers from the Huggingface Transformers library. Dependencies include Numpy and Pillow for image post-processing. Installation can be done using `uv tool` or classic virtual environment setup. Command-line arguments allow for image generation with specified models, prompts, and optional parameters. Quantization options for speed and memory reduction are available. LoRA adapters can be loaded for fine-tuning image generation. Controlnet support provides more control over image generation with reference images. Current limitations include generating images one by one, lack of support for negative prompts, and some LoRA adapters not working.
truss
Truss is a tool that simplifies the process of serving AI/ML models in production. It provides a consistent and easy-to-use interface for packaging, testing, and deploying models, regardless of the framework they were created with. Truss also includes a live reload server for fast feedback during development, and a batteries-included model serving environment that eliminates the need for Docker and Kubernetes configuration.
garak
Garak is a vulnerability scanner designed for LLMs (Large Language Models) that checks for various weaknesses such as hallucination, data leakage, prompt injection, misinformation, toxicity generation, and jailbreaks. It combines static, dynamic, and adaptive probes to explore vulnerabilities in LLMs. Garak is a free tool developed for red-teaming and assessment purposes, focusing on making LLMs or dialog systems fail. It supports various LLM models and can be used to assess their security and robustness.
ell
ell is a lightweight, functional prompt engineering framework that treats prompts as programs rather than strings. It provides tools for prompt versioning, monitoring, and visualization, as well as support for multimodal inputs and outputs. The framework aims to simplify the process of prompt engineering for language models.
garak
Garak is a free tool that checks if a Large Language Model (LLM) can be made to fail in a way that is undesirable. It probes for hallucination, data leakage, prompt injection, misinformation, toxicity generation, jailbreaks, and many other weaknesses. Garak's a free tool. We love developing it and are always interested in adding functionality to support applications.
For similar tasks

LeanAide
LeanAide is a work in progress AI tool designed to assist with development using the Lean Theorem Prover. It currently offers a tool that translates natural language statements to Lean types, including theorem statements. The tool is based on GPT 3.5-turbo/GPT 4 and requires an OpenAI key for usage. Users can include LeanAide as a dependency in their projects to access the translation functionality.
Awesome-LLM-Constrained-Decoding
Awesome-LLM-Constrained-Decoding is a curated list of papers, code, and resources related to constrained decoding of Large Language Models (LLMs). The repository aims to facilitate reliable, controllable, and efficient generation with LLMs by providing a comprehensive collection of materials in this domain.

cline-based-code-generator
HAI Code Generator is a cutting-edge tool designed to simplify and automate task execution while enhancing code generation workflows. Leveraging Specif AI, it streamlines processes like task execution, file identification, and code documentation through intelligent automation and AI-driven capabilities. Built on Cline's powerful foundation for AI-assisted development, HAI Code Generator boosts productivity and precision by automating task execution and integrating file management capabilities. It combines intelligent file indexing, context generation, and LLM-driven automation to minimize manual effort and ensure task accuracy. Perfect for developers and teams aiming to enhance their workflows.
For similar jobs
sweep
Sweep is an AI junior developer that turns bugs and feature requests into code changes. It automatically handles developer experience improvements like adding type hints and improving test coverage.
teams-ai
The Teams AI Library is a software development kit (SDK) that helps developers create bots that can interact with Teams and Microsoft 365 applications. It is built on top of the Bot Framework SDK and simplifies the process of developing bots that interact with Teams' artificial intelligence capabilities. The SDK is available for JavaScript/TypeScript, .NET, and Python.
ai-guide
This guide is dedicated to Large Language Models (LLMs) that you can run on your home computer. It assumes your PC is a lower-end, non-gaming setup.

classifai
Supercharge WordPress Content Workflows and Engagement with Artificial Intelligence. Tap into leading cloud-based services like OpenAI, Microsoft Azure AI, Google Gemini and IBM Watson to augment your WordPress-powered websites. Publish content faster while improving SEO performance and increasing audience engagement. ClassifAI integrates Artificial Intelligence and Machine Learning technologies to lighten your workload and eliminate tedious tasks, giving you more time to create original content that matters.
chatbot-ui
Chatbot UI is an open-source AI chat app that allows users to create and deploy their own AI chatbots. It is easy to use and can be customized to fit any need. Chatbot UI is perfect for businesses, developers, and anyone who wants to create a chatbot.
BricksLLM
BricksLLM is a cloud native AI gateway written in Go. Currently, it provides native support for OpenAI, Anthropic, Azure OpenAI and vLLM. BricksLLM aims to provide enterprise level infrastructure that can power any LLM production use cases. Here are some use cases for BricksLLM: * Set LLM usage limits for users on different pricing tiers * Track LLM usage on a per user and per organization basis * Block or redact requests containing PIIs * Improve LLM reliability with failovers, retries and caching * Distribute API keys with rate limits and cost limits for internal development/production use cases * Distribute API keys with rate limits and cost limits for students
uAgents
uAgents is a Python library developed by Fetch.ai that allows for the creation of autonomous AI agents. These agents can perform various tasks on a schedule or take action on various events. uAgents are easy to create and manage, and they are connected to a fast-growing network of other uAgents. They are also secure, with cryptographically secured messages and wallets.
griptape
Griptape is a modular Python framework for building AI-powered applications that securely connect to your enterprise data and APIs. It offers developers the ability to maintain control and flexibility at every step. Griptape's core components include Structures (Agents, Pipelines, and Workflows), Tasks, Tools, Memory (Conversation Memory, Task Memory, and Meta Memory), Drivers (Prompt and Embedding Drivers, Vector Store Drivers, Image Generation Drivers, Image Query Drivers, SQL Drivers, Web Scraper Drivers, and Conversation Memory Drivers), Engines (Query Engines, Extraction Engines, Summary Engines, Image Generation Engines, and Image Query Engines), and additional components (Rulesets, Loaders, Artifacts, Chunkers, and Tokenizers). Griptape enables developers to create AI-powered applications with ease and efficiency.